- This is an assessment test.
- These tests focus on the basics of Maths and are meant to indicate your preparation level for the subject.
- Kindly take the tests in this series with a pre-defined schedule.
Basic Maths: Test 11
Congratulations - you have completed Basic Maths: Test 11.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
The value of $ \displaystyle 1+\frac{3}{1+\frac{2}{3+\frac{4}{5}}}$
$ \displaystyle \frac{12}{29}$ | |
$ \displaystyle \frac{68}{19}$ | |
$ \displaystyle \frac{86}{29}$ | |
$ \displaystyle \frac{2}{19}$ |
Question 1 Explanation:
$ \displaystyle \begin{array}{l}1+\frac{3}{1+\frac{2}{\frac{15+4}{5}}}\\=1+\frac{3}{1+\frac{2\times 5}{19}}\\=1+\frac{3}{\frac{19+10}{19}}\\=1+\frac{57}{29}=\frac{29+57}{29}=\frac{86}{29}\end{array}$
Question 2 |
Simplify $ \displaystyle \frac{19}{43}\div \frac{1}{2+\frac{1}{3+\frac{1}{1+\frac{1}{4}}}}$
$ \displaystyle \frac{19}{43}$ | |
$ \displaystyle \text{1}$ | |
$ \displaystyle \frac{34}{19}$ | |
$ \displaystyle \frac{45}{43}$ |
Question 2 Explanation:
We can simplified this question as
$ \displaystyle \begin{array}{l}\frac{19}{43}\div \frac{1}{2+\frac{1}{3+\frac{1}{1+\frac{1}{4}}}}\\=\frac{19}{43}\div \frac{1}{2+\frac{1}{3+\frac{4}{5}}}\\=\frac{19}{43}\div \frac{1}{2+\frac{5}{19}}\\=\frac{19}{43}\div \frac{19}{43}\\=\frac{19}{43}\times \frac{43}{19}=1\end{array}$
So the right answer for the question is option b
$ \displaystyle \begin{array}{l}\frac{19}{43}\div \frac{1}{2+\frac{1}{3+\frac{1}{1+\frac{1}{4}}}}\\=\frac{19}{43}\div \frac{1}{2+\frac{1}{3+\frac{4}{5}}}\\=\frac{19}{43}\div \frac{1}{2+\frac{5}{19}}\\=\frac{19}{43}\div \frac{19}{43}\\=\frac{19}{43}\times \frac{43}{19}=1\end{array}$
So the right answer for the question is option b
Question 3 |
The simplification of $ \displaystyle \frac{4}{3+\frac{3}{1-\frac{2}{3}}}$ gives
7 | |
1/3 | |
5/12 | |
7/12 |
Question 3 Explanation:
We can simplified the equation as
$ \displaystyle \begin{array}{l}\frac{4}{3+\frac{3}{\frac{3-2}{3}}}\\=\frac{4}{3+\frac{3}{\frac{1}{3}}}\\\frac{4}{3+3\times 3}\\=\frac{4}{3+9}\\=\frac{4}{12}\\=\frac{1}{3}\end{array}$
So the best option for the question is option b
$ \displaystyle \begin{array}{l}\frac{4}{3+\frac{3}{\frac{3-2}{3}}}\\=\frac{4}{3+\frac{3}{\frac{1}{3}}}\\\frac{4}{3+3\times 3}\\=\frac{4}{3+9}\\=\frac{4}{12}\\=\frac{1}{3}\end{array}$
So the best option for the question is option b
Question 4 |
$ \displaystyle 8=p+\frac{1}{1+\frac{1}{3+\frac{1}{4}}}$, then the value of p is:
$ \displaystyle \frac{191}{17}$ | |
$ \displaystyle \frac{123}{17}$ | |
$ \displaystyle \frac{141}{17}$ | |
$ \displaystyle \frac{133}{17}$ |
Question 4 Explanation:
$ \displaystyle \begin{array}{l}8=p+\frac{1}{1+\frac{1}{3+\frac{1}{4}}}\\\Rightarrow 8=p+\frac{1}{1+\frac{1}{\frac{12+1}{4}}}\\\Rightarrow 8=p+\frac{1}{1+\frac{4}{13}}\\\Rightarrow 8=p+\frac{1}{\frac{13+4}{13}}\\\Rightarrow 8=p+\frac{1}{\frac{17}{13}}\\\Rightarrow 8=p+\frac{13}{17}\,\,\\\Rightarrow \,p=8-\frac{13}{17}\\=\frac{123}{17}\end{array}$
Question 5 |
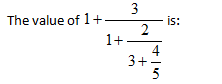
$ \displaystyle \frac{12}{29}$ | |
$ \displaystyle \frac{68}{19}$ | |
$ \displaystyle \frac{86}{29}$ | |
$ \frac{2}{19}$ |
Question 5 Explanation:
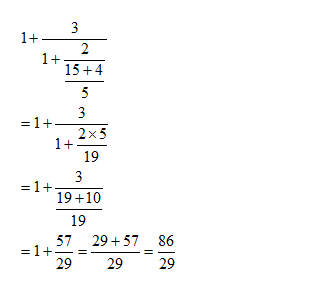
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 5 questions to complete.
List |













