Geometry and Mensuration: Test 28

This is an assessment test.
These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
Kindly take the tests in this series with a pre-defined schedule.

Geometry and Mensuration: Test 28

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Congratulations - you have completed Geometry and Mensuration: Test 28.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%

Your answers are highlighted below.

Question 1

ABCD is a rhombus. AB is produced to F and BA is produced to E such that AB= AE= BF. Also ED and CF are produced to meet at G. Then:

A	ED > CF
B	EG⊥GF
C	ED² +CF²= EF²
D	ED\|\|CF

Question 1 Explanation:

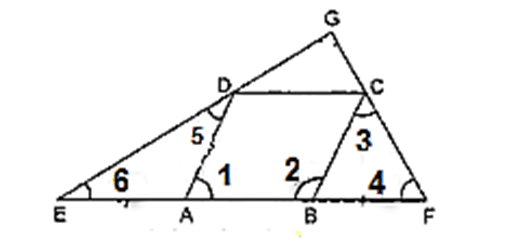height="246"/>
Here AB= AE= BF.......(1)Given ABCD is a rhombus.
Therefore, AB = BC = CD = AD ... (2)
On equating (1) and (2), we get
BC = BF
⇒∠4 = ∠3 [Angles opposite to equal sides are equal]
Again, ∠B is the exterior angle of triangle BFC.
Therefore, ∠2 = ∠3 + ∠4 = 2∠4 ... (3)
Similarly, AE = AD ⇒∠5 = ∠6
Also, ∠A is the exterior angle of triangle ADE
⇒∠1 = 2∠6 ... (4)
Also, ∠1 +∠2 = 180° [consecutive interior angles]
∴ 2∠6 + 2∠4 = 180°
⇒∠6 + ∠4 = 90° ... (5)
Now, in triangle EGF, by angle sum property of triangle
⇒ 90°+ ∠G = 180° [using (5)]
Thus, EG ⊥ FG.

Question 2

Two equal circles of radius 4 cm intersect each other such that each passes through the centre of the other. The length of the common chord is:

A	$ \displaystyle 2\sqrt{3}$
B	$ \displaystyle 4\sqrt{3}$
C	$ \displaystyle 2\sqrt{2}$
D	$ \displaystyle 8$

Question 2 Explanation:

$ \begin{array}{l}The\text{ }length\text{ }of\text{ }the\text{ }common\text{ }chord\text{ }=\text{ }\\2\text{ }\times \text{ }length\text{ }of\text{ }the\text{ }altitude\text{ }of\text{ }the\text{ }equilateral\text{ }triangle\text{ }of\text{ }side\text{ }4\text{ }cm.\\Thus\text{ }the\text{ }length\text{ }of\text{ }common\text{ }chord\text{ }is\\2\times \frac{\sqrt{3}}{2}\times 4\\=4\sqrt{3}\end{array}$

Question 3

The length of two chords AB and AC of a circle are 8 cm and 6 cm and ∠BAC= 90^o, then the radius of circle is

A	25 cm
B	20 cm
C	4 cm
D	5 cm

Question 3 Explanation:

$ \begin{array}{l}The\text{ }diameter=\sqrt{{{8}^{2}}+{{6}^{2}}}=10\\Thus\text{ }the\text{ }radius\text{ }=5.\end{array}$

Question 4

The tangents are drawn at the extremities of a diameter AB of a circle with centre P. If a tangent to the circle at the point C intersects the other two tangents at Q and R, then the measure of the ∠QPR is