We all have studied about basic division concepts. In this article, we will further extend this concept to understand factors and multiples.
Factors:
If an integer x is completely divided by another integer y, then x is said to be a multiple of y; and y is said to be a factor of x.
Let us take an example to understand it better.
Example:
12 is a multiple of 3 as it divides 12 four times and 3 is a factor of 12.
But 12 cannot be a multiple of 7 as 12 cannot be divided by 7 completely.
Next we move on to the calculation of the total number of factors.
Total Number of Factors of a Number:
A composite number N can be written as a product of its prime factors.
If N can be written as ![]() then total number of factors will be
then total number of factors will be ![]() .
.
(Where a, b, c are prime numbers)
But where did this formula come from? Let us understand by taking an example.
Example: Take N = 300
Prime factors of N= ![]()
Now if a number D is to divide N, maximum value of D can be = ![]() and minimum can be
and minimum can be

Now that we have calculated the total number of factor, let us see how many of those are even and how many are odd.
Finding ODD and EVEN Factors of a Number:
Even Factors:
Example: Let us take an example of N = 240
N= 240= ![]()
To make any factor EVEN, 2 or any of its power has to be a multiple of it, otherwise odd*odd can give a odd number. For eg:
2*3=6; *5=20 are even factors, because they are getting multiplied with 2 or with its powers.
But in case we don’t include 2, then
3*5 =15 ; *5 = 5
So, if even factors are to be calculated we need to exclude and include all other powers of 2 while making combinations.
Let D be a possible factor of N, then
D= ![]()
In this case, total no of even factors will be = 4 * (1+1)*(1+1) = 16
Odd factors:
Again we will take example of N= 240
Unlike the above-discussed solution, in this case only power included of 2 will be ![]()
So N= 240= ![]()
Odd factors :- 1*(1+1)*(1+1)=4
With everything studied so far, you need to keep the following in mind:
NOTE 1:
We know that total no. of factors of 240 will be= 5*2*2=20
Using 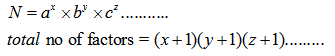
In this case =>
Total no of factors = even factors + odd factors
20= 16+4
So after calculating even factors we can subtract them from total number of factors to get number of odd factors.
NOTE 2:
Keep in mind that number of odd factors won’t be equal to the number of even factors. Usually we tend to take the number of odd/even factors as half of the total number of factors. But that won’t be the case.
Let’s try some questions based on the above-discussed concepts.
EXERCISE:
Question 1: Find the total number of factors of 58800.
(1) 90
(2) 80
(3) 180
(4) 45
Answer and Explanation
Solution: option (1)
We first factorize 58800.
58800 = 24 315272
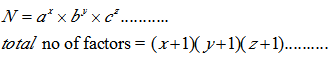
Total number of factors = (4+1)(1+1)(2+1)(2+1)=90
Question 2: Find the number of even factors of 58800.
(1) 90
(2) 72
(3) 18
(4) 45
Answer and Explanation
Solution: option (2)
We first factorize 58800.
58800 = 24 315272
To calculate even factors we exclude 20
So total, number of even factors will be= (4)(1+1)(2+1)(2+1)=72
Question 3: Find the number of odd factors of 58800.
(1) 90
(2) 72
(3) 18
(4) 45
Answer and Explanation
Solution: option (3)
We first factorize 58800.
58800 = 24 315272
Number of odd factors = total no of factors – number of even factors
Number of odd factors = 90 -72 = 18
Question 4: Find the number of even factors of 840.
(1) 32
(2) 72
(3) 24
(4) 48
Answer and Explanation
Solution: Option (3)
We first factorize 840.
![]()
To calculate even factors we exclude 20
So total, number of even factors will be= (3)(1+1)(1+1)(1+1)=24
Question 5: Find the number of odd factors of 840.
(1) 8
(2) 7
(3) 18
(4) 32
Answer and Explanation
Solution: Option (1)
We first factorize 58800.
![]()
Total no of factors = 4*2*2*2=32
Number of odd factors = total no of factors – number of even factors
Number of odd factors = 32-24 = 8









