To solve questions based on number system quickly, you should have a good hold of the properties of numbers. Therefore, in this concept article we shall discuss the following handy list of tips that you can remember about numbers (think about each one of these):
Properties of Number line and Numbers:
- The number line goes on till infinity in both directions, which is indicated by the arrows.
- The numbers on the number line are indicated by their respective signs. The number line includes positive and negative numbers, and zero.
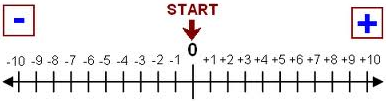
- The integer zero is neutral and neither positive or negative.
- The number in the halfway of 1 and 2 is 1.5 and in the half way of -1 and -2 is
-1.5.
- Between two rational numbers we can always find a rational number.
For e.g. If there are two rational numbers 2 and 3 , there will always be a rational no. between them.
- Numbers, which are either terminating decimals or non-terminating but recurring decimals, are rational numbers. Similarly, numbers, which are non-terminating non recurring decimals are irrational numbers.
- Set of natural numbers is contained in set of whole numbers which is contained in the set of integers which is contained in set of rational numbers which is further contained in set of real numbers, which is further contained in set of complex numbers.
- Addition as well as product of two real numbers is a real number.
- Two real numbers can be added or multiplied in either order i.e. Addition and multiplication of real numbers is commutative. (Order doesn’t matter)
For e.g. if there are two numbers 2 and 3 then 2 + 3 = 3 + 2
- Two real numbers cannot be subtracted or divided in either order i.e. Subtraction and Division of real numbers is not commutative. (Order matters)
For e.g. if there are two numbers 2 and 3, then ![]()
Properties of Zero
Zero is a very important number and has some peculiar properties. Let’s take a look at its properties.
- a x 0 = 0 always for any real number a.
- a + 0 = a always for any real number a.
- a – 0 = a always and 0 – a = -a for any real number a.
- 0/a = 0 when “a” is a non-zero real number.
- a/0 is not defined i.e. we don’t define division by zero.
- a0=1 for any non-zero real number a.
- 00 is not defined.
Properties of Addition of Natural Numbers:
- Sum of first n natural numbers =

Derivation :-
Let us first understand this by an example . We will generalize this later.
Suppose we have to find sum of 1,2,3,4,5,6 . We know that this is an arithmetic series . In arithmetic series, first no. + last no. = second +second last = third +third last .. so on.
1+ 6 =2 + 5 =3 + 4
In each group the sum is 7 . The total number of groups made by 6 numbers are 3.
So, sum of the numbers = 7 × 3 = 21
Now, let us generalize this method.
First n natural numbers= 1,2,3, …………………. (n-2),(n-1),n
We know that this is an arithmetic series. In arithmetic series, first no. + last no. = second number +second last number = third number +third last number .. so on.
1+n =2+n-1=3+n-2 =……
This can be simplified as n+1=n+1=n+1 = ……
In each group, the sum is n+1. Total number of groups made by n numbers are n/2
So, the sum is![]()
- Sum of first n even numbers =>
Derivation: –
Series of even numbers will 2+4+6+8……… 2n
This is an arithmetic series
Sum of arithmetic series =![]()
Sum of arithmetic series = 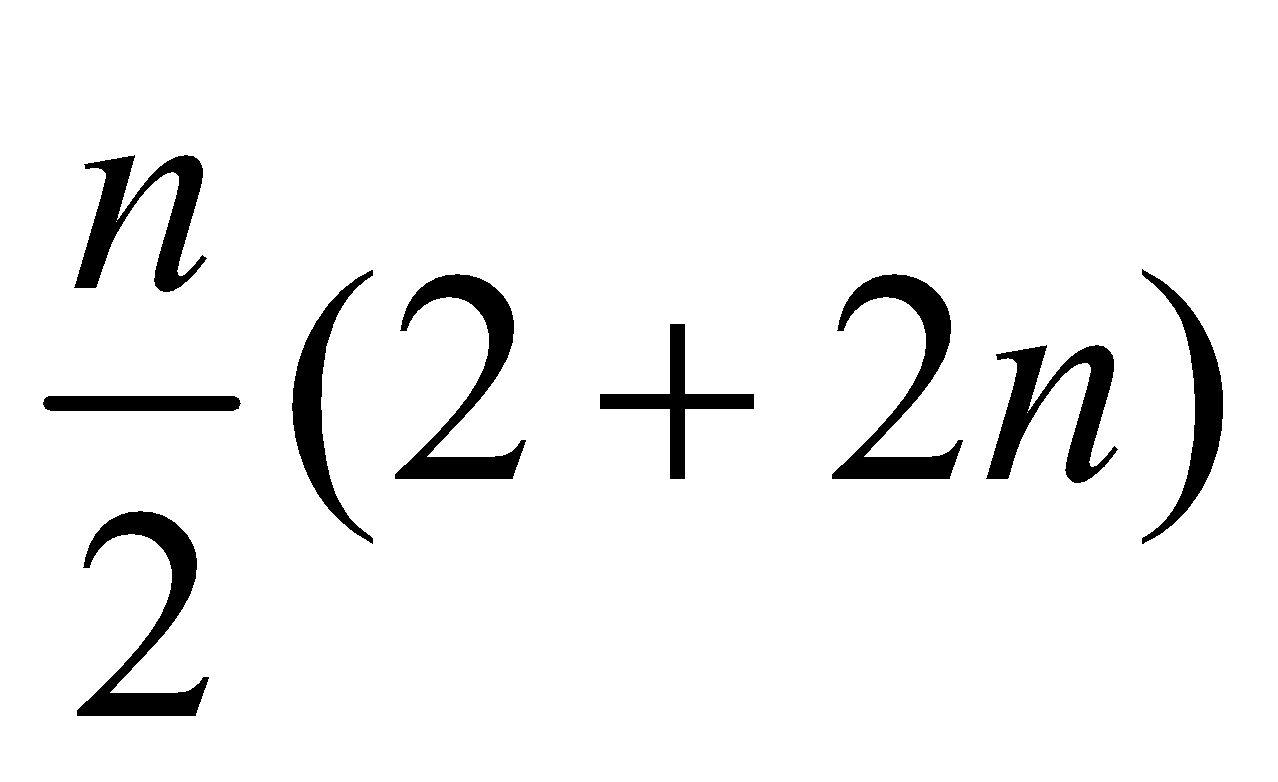 =n(n+1)
=n(n+1)
- Sum of first n odd numbers =

Derivation :-
Series of odd numbers will 1+3+5+……….(2n-1)
This is an arithmetic series
Sum of arithmetic series =![]()
Sum of arithmetic series =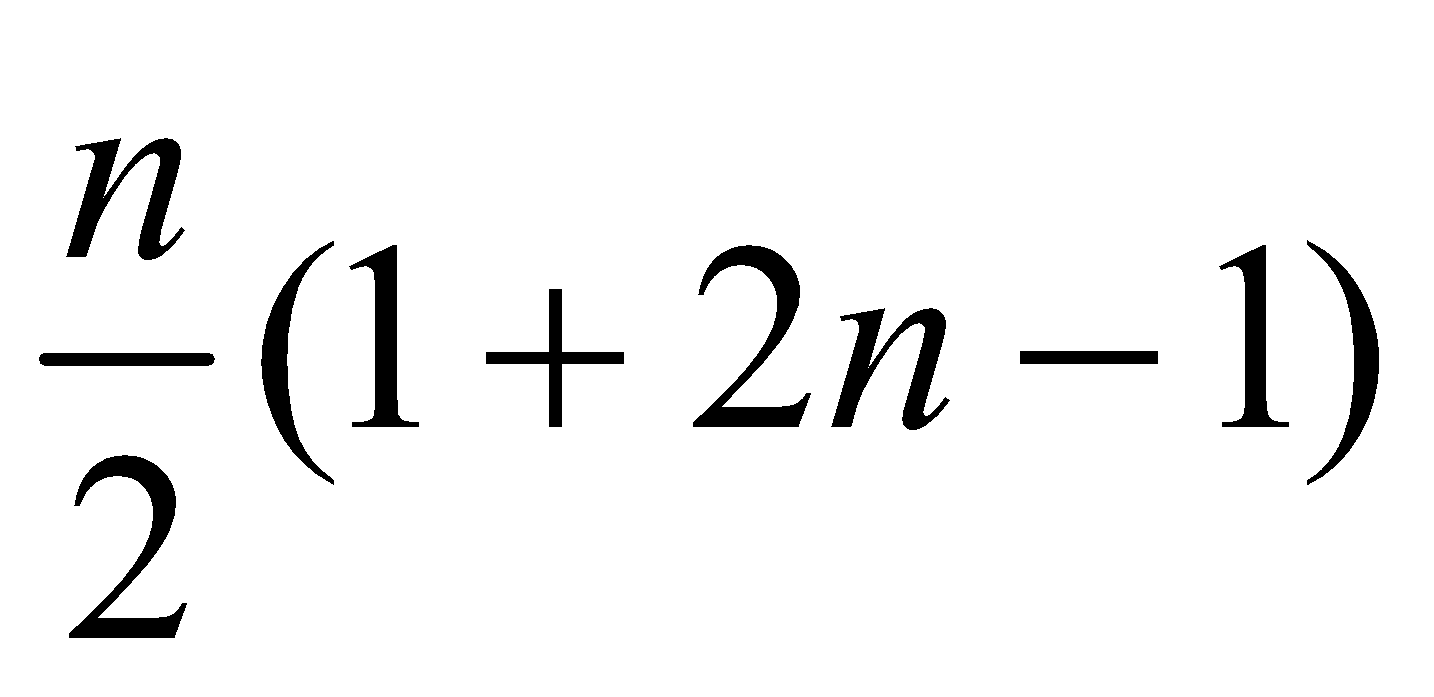 =
=![]()
- Sum of squares of first n natural numbers =>

- Sum of cubes of first n natural numbers =>



- Sum of cubes of 1st ‘n’ Odd natural number = 13 + 33 + 53 + ….. + (2n -1)3 = n2 (2n2 -1)
- Sum of cubes of 1st ‘n’ Even natural number = 23 + 43 + 63 + ….. + (2n)3 = 2 [n (n + 1)]2
Tip: Remember the above-mentioned formulas by heart. They have a wide application in not just number system but in other topics of quant as well.
Some examples for the above properties:
Find the sum of:
(A) First 30 natural numbers
(B) Squares of first 30 natural numbers
(C) Cubes of first 30 natural numbers
(D) First 30 odd natural numbers
(E) Squares of first odd 30 natural numbers
(F) Squares of first even 30 natural numbers
(G) Cubes of first odd 30 natural numbers
(H) Cubes of first even 30 natural numbers
Solution:
(A) 1 + 2 + 3 +…………………..+ 29 + 30 = ![]() = 15 × 31 = 465
= 15 × 31 = 465
(B) 12 + 22 + 32 + ….. + 302 = ![]() = 5 × 31 × 61 = 9455
= 5 × 31 × 61 = 9455
(C) 13 + 23 + 33+ ….. + 303 = ![]() = (15 × 31)2 = 216225
= (15 × 31)2 = 216225
(D) 1+ 3 + 5 + ………. + 57 + 59 = 302 = 900
(E) 12 + 32 + 52 + ….. + (59) 2 = ![]() = 10 ×59 × 61= 35990
= 10 ×59 × 61= 35990
(F) 22 + 42 + 62 + ….. + 602 = ![]() = 20(31)(61)= 37820
= 20(31)(61)= 37820
(G) 13 + 33 + 53 + ….. + (59)3 = 302× (2(30)2 -1) =1619100
(H) 23 + 43 + 63 + ….. + 603 = 2 × [30 × 31]2 = 2 × [30 × 31]2 =1729800
Let us practice more questions.
EXERCISE:
Question 1: Find the sum of first 20 odd natural numbers.
a. 400
b. 200
c. 4000
d. 420
Answer and Explanation
Solution: Sum of first n odd numbers =![]()
So, the sum of first 20 odd natural numbers = 202 = 400. Hence, option (a)
Question 2: Find the sum of first 20 even numbers.
a. 400
b. 200
c. 4000
d. 420
Answer and Explanation
Solution: Sum of first n even numbers =![]()
So, the sum of first 20 even natural numbers = 20 × 21 = 420
Hence, option (d)
Question 3: Find the sum of first 10 natural numbers.
a. 55
b. 110
c. 220
d. 100
Answer and Explanation
Solution: Sum of first ‘n’ natural numbers =![]()
So, the sum of first 10 natural numbers =![]() .Hence, option (a)
.Hence, option (a)
Question 4: Find the sum of cubes of first 20 odd natural numbers.
a. 419600
b. 319600
c. 960000
d. 628000
Answer and Explanation
Solution: The sum of cubes of first n odd natural numbers = n2 (2n2 -1)
So, the sum of cubes of first 20 odd natural numbers = 202(2 × 202 – 1) = 400 × 799 = 319600
Hence, option (b)
Question 5: Find the sum of cubes of first 20 even natural numbers.
a. 319600
b. 352800
c. 705600
d. 420000
Answer and Explanation
Solution: The sum of cubes of first n even natural numbers = 2 [n (n + 1)]2
So, the sum of cubes of first n even natural numbers = ![]() =352800
=352800
Hence, option (b)









