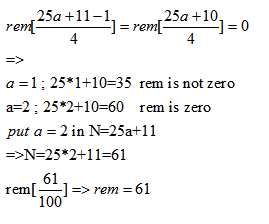Remainder

This article further covers the ways to calculate remainders.

 Remainder Theorem:

Remainder theorem states that when a polynomial function f(x) is divided by (x –a) where a is a constant, it will give us a remainder f(a).

Remainder of

Let us understand this with the help of some examples.

Example: Find the remainder of 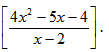Solution:

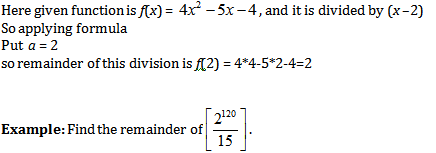
Solution:

Method 1:

Here, note that numerator is in the form of powers of 2 hence we have to convert the denominator also in the form of powers of 2. Here denominator 15 = 2⁴ –1

Now denominator is in the form of 2⁴, so we can  write numerator also in the form of 2⁴.

2¹²⁰ =  (2⁴)³⁰. Now if take    2⁴ = x

then numerator => x³⁰

denominator = x –1.

Now by applying remainder theorem concept

a = 1 so remainder is f(a) =  (1)³⁰ = 1.

Chinese Remainder Theorem:

Chinese theorem is used when we have a big composite number in denominator and complex power in numerator.

Let us understand this with the help of some examples:

 Case 1: When remainder obtained by both numbers is equal

 Example: Find the remainder of

Solution:

Step 1:

Write the denominator as product of two coprimes

In this case 15 = 5 * 3

And dedude remainder for respective factor

Step 2:

Case 2: When remainders obtained by both numbers are unequal

 Example: Find the remainder of

Solution:

Step 1:

Step 2:

Now we need values of a and b for that N is same

Try out some more questions based on this concept so as to get a good hold of this topic.

EXERCISE:

Question 1. Find the remainder of .

(1) 22

(2) -22

(3) 11

(4) 0

Question 2. Find remainder of .

(1) 12

(2) 32

(3) 162

(4) 0

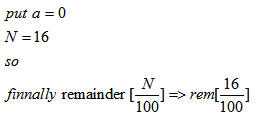
Question 3. Find remainder of 

(1) 37

(2) 52

(3) 16

(4) 61