How do we proceed when we are asked to check whether a prime number is divisible by a given number or not? It can be done using the concept of seed numbers. Let’s see what this is.
Method:
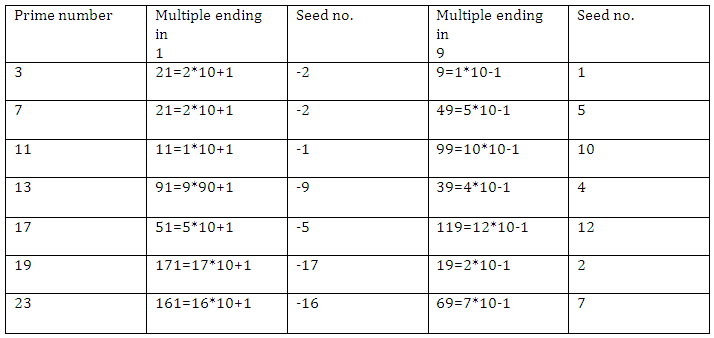
Every odd prime number gives unit digit of 1 and 9 in two of their first 10 multiples.
Let’s try to understand this with an example:
3*3=9 and 3*7 =21; in first 10 multiples of 3, third multiple is 9 and 7th multiple is 21.
Both end in unit digit of 9 and 1.
17*3=51 and 17*7=119; in first 10 multiples of 7 third multiple is 51 and 7th multiple is 119
Both end in unit digit of 9 and 1.
We can write 9, 21, 51 and 119 in a multiple form of 10.
9=1*10-1
21=2*10+1
51=5*10+1
119=12*10-1
The numbers that are multiplied by 10 are seed numbers for that particular prime number.
For example:
17*3=51 =5*10+1 ( in this case 5 is multiplied by 10 so we revert it’s sign to -5 and -5 is seed no for 17)
17*7=119=12*10-1 ( in this case 12 is multiplied by 10 so 12 is also a seed no for 1)
** We revert sign of seed number in case of 10n+1; sign remains the same in case of 10n-1
List of seed numbers:
Process to use seed number and check divisibility: –
Example: Check whether 1768 is divided by 17.
Solution:
Step 1:- Multiply unit digit of number with the seed number of divisor. In this case seed number can be: -5 or 12 .
Step 2:- 8 *-5= – 40 ; now add this in the remaining number to the left of unit digit =>
176+ (-40)=136
Keep repeating the process till you are left with single digit. And check whether it is divided by the given divisor.
So multiply unit digit 6 with -5, 6*-5=-30
13+(-30)=-17
Which is divisible by 17.













