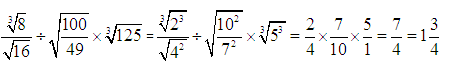Every year we have seen questions in CAT and other MBA entrance exams involving direct or indirect application of cubes or cube roots. It has vast applications. Therefore let’s get started with this concept.
Cube of a Number:
For a given number x, we define, cube of x = x × x × x, denoted by x3.
Example:
(i) 43 = (4×4×4) = 64. Thus, cube of 4 is 64.
(ii) 53 = (5×5×5) = 625. Thus, cube of 5 is 625.
Perfect Cube:
A given natural number is a perfect cube if it can be expressed as the product of triplets of equal factors i.e. if you can make pair of triplets from prime factors of a number, the number will be a perfect cube.
Let us understand this with the following examples: –
Example 1: Show that 180 is not a perfect cube.
Solution: Resolving 180 into prime factors, we get:
![]()
We cannot make triplets from these prime factors, so this is not a cube.
Example 2: Show that 216 is a perfect cube. Also, find the number whose cube is 216.
Solution: Resolving 216 into prime factors, we get:
216 = 2×2×2×3×3×3 = (2×3) ×(2×3) ×(2×3) = (6×6×6)=(6)3.
Thus, 216 is a perfect cube.
And, 6 is the number whose cube is 216.
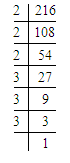
Cubes of Negative Integers:
What would be the cube of a negative number? Let’s find out! The cube of a negative integer is always negative.
Example:
(–1)3 = (–1) × (–1) × (–1) = –1,
(–2)3 = (–2) × (–2) = –8,
(–3)3 = (–3) × (–3) × (–3) = –27, etc.
Cube Of A Rational Number:
How do we go about finding the cube of a rational number?
Well, this is shown below along with the help of examples,
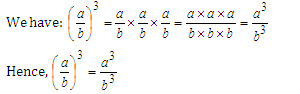
Example 1:
Find the cubes
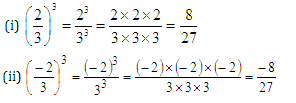
Example 2:
Find the cube of each of the following:
![]()
Solution:
We have:
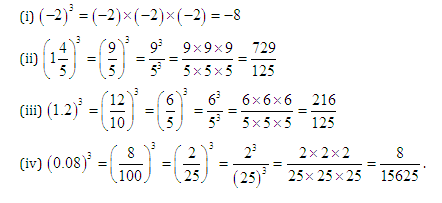
Properties Of Cubes Of Numbers:
Let us look at the characteristic properties that Cubic numbers posses.
(i) The cube of every even number is even.
For example: 23=8, which is even. Similarly, 43=64, which again is even.
(ii) The cube of every odd number is odd.
For example: 33=27, which is odd. Similarly, 53=125, which again is odd.
Cube Roots:
The cube root of a number x is that number whose cube gives x.
We denote the cube root of x by ![]()
Example 1:
(i) Since (2×2×2) = 8, we have ![]()
(ii) Since (5×5×5) = 125, we have ![]()
These were some small numbers whose cube roots are on fingertips. But what if the number is large or unfamiliar?
You could follow the procedure shown below to find the Cube root.
Method of finding the cube root of a given number by factorization:
Step 1. Express the given number as the product of primes.
Step 2. Make groups in triplets of the same prime.
Step 3. Find the product of primes, choosing one from each triplet.
Step 4. This product is the required cube root of the given number.
Example 2: Evaluate ![]()
Solution:
By prime factorization, we have
2744 = 2 × 2 × 2 × 7 × 7 × 7
= (2 × 2 × 2) × (7 × 7 × 7)
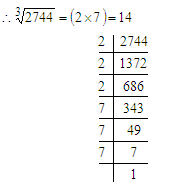
Cube Root of A Negative Perfect Cube:
Let “a” be a positive integer.
Then, (–a) is a negative integer.
We know that (–a)3 = –a3.
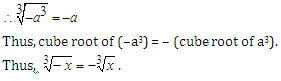
Example: Find the cube root of (–1000).
Solution: We know that ![]()
Resolving 1000 into prime factors, we get
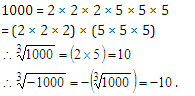
Cube Root of Product of Integers:
We use this concept: ![]()
Example: Evaluate ![]()
Solution: We have: 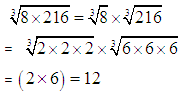
Cube Root of A Rational Number:
We use this concept: 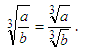
Example:
Evaluate: 
Solution:
We have:
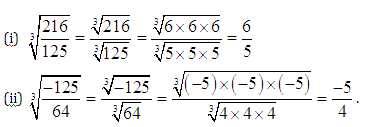
Let’s solve some more questions based on the same concept.
EXERCISE:
Question 1: By which smallest number should1323 be multiplied, so that it becomes a perfect cube?
(1) 2 (2) 3 (4) 5 (4) 7
Answer and Explanation
Solution: (4)
Prime factorize 1323
![]()
To make it a perfect cube, we need to express the product in form of triplets. 3 is in form of triplets and to make a triplet of 7, we need to multiply the term by 7 .
So, it must be multiplied by 7.
Question2: The smallest positive integer n, for which 864n is a perfect cube, is:
(1) 1 (2) 2 (3) 3 (4) 4
Answer and Explanation
Solution: (2)
Firstly prime factorize 864
864 = 23 × 33 × 22
To make the perfect cube, we need to express the product in form of triplets. So, we need to multiply the term by 2.
For 864n to be a perfect cube, n should be 2.
Question3: The least number that must be added to 1720 so as to obtain a perfect cube is
(1) 7 (2) 8 (3) 11 (4) 13
Answer and Explanation
Solution: (2)
This question requires a little bit hit and trial method. We need to find a cube near 1720, which is
12 ×12 × 12 = 1728
So we need to add 8 in 1720 to make it 1728.
Question4: The sum of the cubes of the numbers 22, –14 and –8 is equal to
(1) 7392 (2) 9630 (3) 6436 (4) 0
Answer and Explanation
Solution: (1)
We know that a2 + b3 + c3 = 3abc, if a + b + c = 0
Here, 22 – 14 – 8 = 0
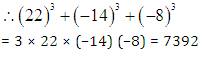
Question5: 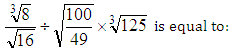
![]()
Answer and Explanation
Solution: (2)