Problems related to trains:
The problems related to the trains is a common area from which the questions are asked in the examinations. There are certain things that are given below, which should be kept in mind while dealing with the problems related to the trains.
- The length of the train is usually given in the meters whereas its speed is given in km/hr. So, you should always be careful regarding the units taken. In most of the cases you need to change the units of speed from km/hr to m/sec.
- If a train crosses a stationary point object (an object whose dimensions are negligible as compared to the dimensions of the train) like a pole, tree, or a man etc. then in that case the distance travelled by the train is same as the length of the train.
- When a train crosses another train, platform, bridge, tunneletc. then the distance traveled is the length of the train + length of the second train/ platform / bridge/ tunnel.
Example:How much time will a train 100m long running at the rate of 18km/hr will take to pass a man?
Solution:Here the distance = length of train. Now the speed of the train is in km/hr whereas the length of the train is in meters. So, we will convert the speed in m/sec.
![]()
![]()
Example: How long does a train 100 meter long running at a rate of 18km/hr take to cross a bridge 200 m in length?
Solution: The total distance covered will be length of train + length of bridge =100+200=300m. The speed of the train is in km/hr. whereas the distance travelled by the train is in meters. So, we will convert the speed in m/sec.
![]()
![]()
Example: A train with 54km/hr. crosses a bridge in 36 seconds.Another train 100m shorter crosses the same bridge at 36km/hr.Find the time taken by the second train to cross the bridge.
Solution: Speed of the first train =![]()
Speed of second train =![]()
Let the length of the first train is ‘x’ meter and that of the second is ‘x – 100’ meter. Let the length of the bridge is ‘y’ meter.
The distance travelled by the first train while crossing the bridge = 15 × 36 = 540 m
Time taken by second train to cross the bridge
![]()
Solve the exercise given below to get the concepts clear.
EXERCISE:
Question 1: A man walking at the rate of 5 km/hr. crosses a bridge in 15 minutes. The length of the bridge (in meters) is:
(1) 600
(2) 750
(3) 1000
(4) 1250
Answer and Explanation
Solution: (4)

Question 2: The length of a train and that of a platform are equal. If with a speed of 90 km/hr the train crosses the platform in one minute, then the length of the train (in meters) is:
(1) 500
(2) 600
(3) 750
(4) 900
Answer and Explanation
Solution: (3)
Let the length of train be x meters.
Speed = 90 km/hr.![]()
Distance covered = 25 × 60 = 1500 m
Now 2x = 1500
⇒ x = 750 m
Question 3: Atrain passes two bridges of lengths 800 m and 400 m in 100 seconds and 60 seconds, respectively. What is the length of the train?
(1) 80 m
(2) 90 m
(3) 200 m
(4) 150 m
Answer and Explanation
Solution: (3)
Let the length of the train = x m
Length of first bridge =800m
Since train passes the 800 m bridge in 100 seconds
Speed of the train =![]()
Again, train passes the 400 m bridge in 60 seconds.
⇒ Speed of the train =![]()
Now![]()
⇒ 3x + 2400 = 5x + 2000
⇒ 2x = 400
⇒ x = 200 m
Question 4: A 150-metre-long train crosses a 500 meters long bridge in 30 seconds. What time will it take to cross a platform 370 meters long?
(1) 36 seconds
(2) 30 seconds
(3) 24 seconds
(4) 18 seconds
Answer and Explanation
Solution: (3)
Let the length of train be x and length of platform be y
![]()
The time taken in the second case =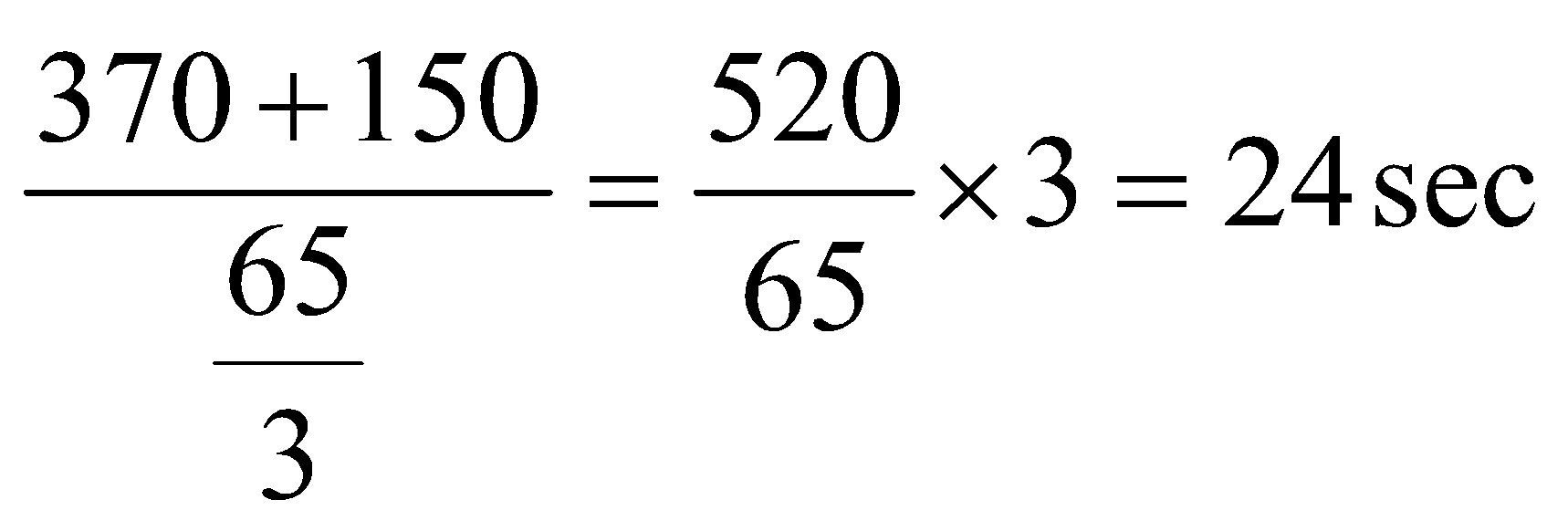
Question 5: A train 800 meters long is running at the speed of 78 km/hr. If it crosses a tunnel in 1 minute, then the length of the tunnel (in meters) is:
(1) 720
(2) 500
(3) 1300
(4) 13
Answer and Explanation
Solution: (2)
When a train crosses a tunnel, it covers a distance equal to the sum of its own length and tunnel.
Let the length of tunnel be zmeters.
Speed = 78 km/h =![]()

∴Length of tunnel = 500 meters.
Question 6: A train with a uniform speed passes a platform, 122 meters long, in 17 seconds and a bridge, 210 meters long, in 25 seconds. The speed of the train is:
(1) 46.5 km/hour
(2) 37.5 km/hour
(3) 37.6 km/hour
(4) 39.6 km/hour
Answer and Explanation
Solution: (4)
Let the length of the train = x meter.
According to the question, in crossing both the platform speed is same so
Speed of the train

Speed Time Distance Questions: Problems on Speed Time Distance you should solve for competitive examination preparation
Welcome to this exercise on Speed Time Distance. In this exercise, we build on the basic concepts for Speed Time Distance and focus on trains. As you prepare for your competitive examinations, you will come across questions on Speed Time Distance with focus on trains. Such questions based on trains need optimized tackling and can be solved with ease by using simple tricks and understanding the relationships highlighted in this Speed Time Distance Questions article. The Speed Time Distance Questions exercise comes into the picture where it gives you a chance to practice the highlighted and important concepts related to this Speed Time Distance and trains question type.













