Trigon: The Root of Triangles in Mathematics and Beyond
Explore the fascinating journey of the word root "Trigon," derived from Greek, meaning "triangle." From trigonometry, the cornerstone of geometry, to trigon, a historical and mathematical term, this root has left its mark on both the ancient and modern worlds.
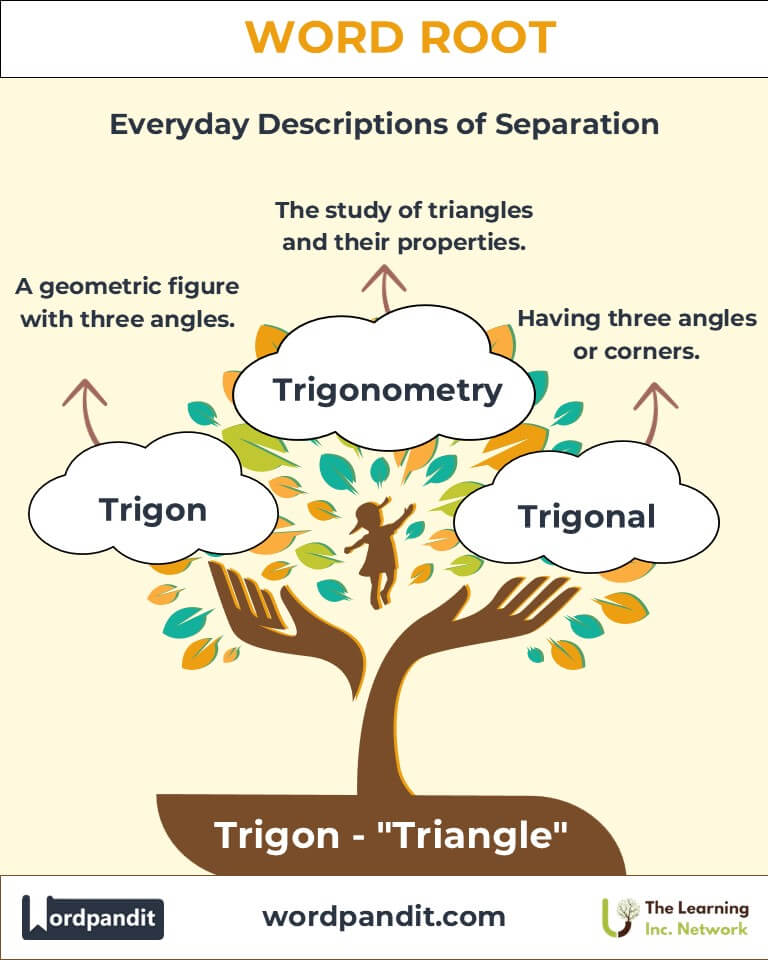
Table of Contents
- Introduction: The Significance of Trigon
- Etymology and Historical Journey
- Mnemonic: Unlocking the Power of Trigon
- Common Trigon-Related Terms
- Trigon Through Time
- Trigon in Specialized Fields
- Illustrative Story: Trigon in Action
- Cultural Significance of the Trigon Root
- The Trigon Family Tree
- FAQs about the Trigon Word Root
- Test Your Knowledge: Trigon Word Root Quiz
- Conclusion: The Enduring Geometry of Trigon
Introduction: The Significance of Trigon
Have you ever wondered how ancient mathematicians calculated distances without advanced technology? The answer often lies in the root "Trigon," meaning "triangle" in Greek. Pronounced "TRY-gon," this root forms the basis of essential mathematical concepts such as trigonometry, the study of triangles and their properties. Whether in architecture, astronomy, or navigation, Trigon connects the simplicity of three-sided shapes to complex real-world applications.

Etymology and Historical Journey
The root "Trigon" originates from the Greek words "tri-" (three) and "gonia" (angle). Ancient Greek mathematicians like Euclid and Pythagoras used triangles to develop early theories of geometry and proportions. The term traveled through Latin as "trigonum," influencing modern European languages. Its association with trigonometry dates back to the Hellenistic period, where it helped astronomers chart celestial paths and predict planetary movements.
Mnemonic: Unlocking the Power of Trigon
Picture a triangular road sign pointing in three directions—each angle representing an aspect of the word root. This simple yet powerful image reminds you of Trigon’s meaning and its centrality in studying angles and triangles.
Mnemonic Device: "Trigon—a triangle pointing the way to mathematical discoveries!"
Common Trigon-Related Terms
- Trigonometry (try-guh-NOM-uh-tree): The branch of mathematics dealing with the relationships between triangle angles and sides.
Example: "Trigonometry is essential for calculating the height of mountains." - Trigon (TRY-gon): A geometric figure with three angles; sometimes refers to triangular structures or tools.
Example: "The trigon in the ancient temple's design reflected symmetry and balance." - Trigonal (TRY-guh-nuhl): Having three angles or corners.
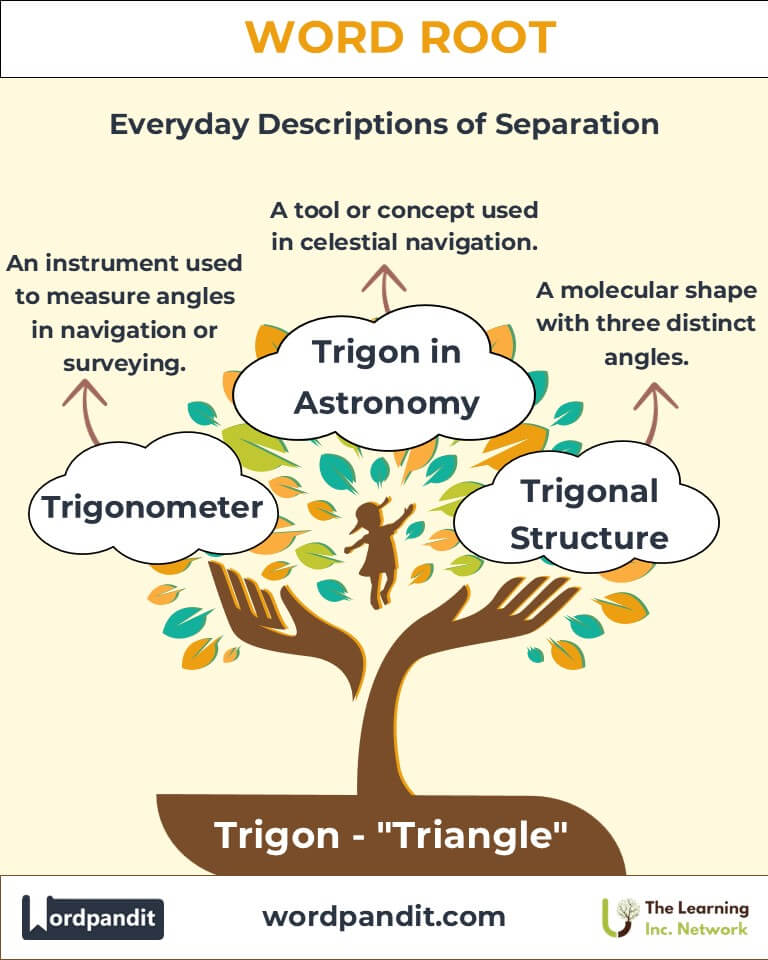
Example: "The trigonal shape of the molecule influences its chemical properties." - Trigonometer (try-GON-uh-muh-ter): An instrument used to measure angles in navigation or surveying.
Example: "Early trigonometers helped sailors chart unknown waters."
Trigon Through Time
- Ancient Applications: Early Greek mathematicians used triangles to understand the relationships between celestial bodies. The term "trigonum" appeared in Roman engineering manuals, emphasizing its role in constructing bridges and aqueducts.
- Modern Evolution: Today, trigonometry is indispensable in fields like robotics, where precise angular calculations ensure accurate motion and design.
Trigon in Specialized Fields
- Mathematics:
Trigonometry remains foundational, solving problems involving waves, cycles, and angles.
Example: Engineers rely on trigonometric functions to design sturdy structures. - Astronomy:
Celestial navigation uses trigonometry to calculate distances between stars and planets.
Example: Astronomers charted lunar eclipses using ancient trigonometric tables. - Medicine:
Imaging technologies like MRIs depend on trigonal symmetry to produce accurate scans.
Example: The trigonal crystal lattice in X-ray diffraction reveals molecular structures.
Illustrative Story: Trigon in Action
In ancient Alexandria, an aspiring astronomer named Callista sought to measure the height of a distant lighthouse. Using a simple trigon, she calculated the angles of elevation at two different points. With her knowledge of trigonometry, she deduced the lighthouse’s exact height, earning admiration for her ingenuity. Callista’s story reminds us of Trigon’s timeless practicality.
Cultural Significance of the Trigon Root
Triangles symbolize stability, balance, and connection across cultures. The Trigon appears in architecture, from Egyptian pyramids to Gothic cathedrals, and serves as a motif in art and religious symbols, like the Trinity. Its mathematical applications have advanced civilizations, guiding trade routes, and inspiring scientific breakthroughs.

The Trigon Family Tree
- Tri- (three):
Examples: Triangle, Trilogy. - Gonia (angle):
Examples: Polygon, Pentagon. - Meter (measure):
Examples: Perimeter, Diameter.
FAQs About " Trigon "
Q: What does "Trigon" mean?
A: The root "Trigon" comes from the Greek words "tri-" (three) and "gonia" (angle), meaning "triangle." It refers to any shape, concept, or tool associated with three angles, such as triangular structures in geometry or ancient trigonometric tools.
Q: What is trigonometry?
A: Trigonometry is the branch of mathematics that studies triangles, particularly the relationships between their angles and sides. Derived from "Trigon" and "metron" (measure), it has practical applications in fields like navigation, engineering, and physics, enabling precise calculations in both theoretical and real-world problems.
Q: What is a trigonal structure?
A: A trigonal structure is one with three distinct angles or corners, commonly seen in geometry and chemistry. For instance, certain molecules, like boron trifluoride, form trigonal planar structures, where three atoms are symmetrically arranged around a central atom.
Q: What role does "Trigon" play in astronomy?
A: In astronomy, trigonometry helps calculate distances between celestial bodies and map their movements. For instance, ancient astronomers used triangular calculations to predict eclipses and locate stars. The trigon was also a tool used in early star charting.
Q: Why are triangles considered stable in construction?
A: Triangles distribute weight evenly and resist deformation, making them the most stable shape in engineering and architecture. For example, bridges and towers often use triangular trusses to ensure durability under heavy loads.
Q: How does trigonometry assist in navigation?
A: Trigonometry allows navigators to measure distances and plot courses by using angles and sides of triangles. Early mariners used trigonometric tables and tools like the trigon to determine their positions relative to stars or landmarks.
Q: What are practical uses of trigonometry today?
A: Trigonometry is crucial in diverse fields such as surveying (measuring land), physics (analyzing wave functions), computer graphics (rendering 3D images), and medicine (analyzing MRI images). Its fundamental role in understanding angles and distances ensures its ongoing importance.
Test Your Knowledge: " Trigon " Mastery Quiz
1. What does the root "Trigon" signify?
2. Which term describes the study of triangle properties?
3. What is a trigonal molecule?
4. What does a trigon measure in navigation?
5. Which civilization advanced the use of trigonometry?
Conclusion: The Enduring Geometry of Trigon
The root Trigon continues to shape our understanding of the world, from calculating planetary orbits to designing modern skyscrapers. Its simplicity as a triangle belies its profound impact across disciplines, reminding us of the enduring power of geometry. Let Trigon inspire you to explore the connections between angles, shapes, and the universe.












