Geometry and Mensuration: Test 18

This is an assessment test.
These tests focus on geometry and mensuration and are meant to indicate your preparation level for the subject.
Kindly take the tests in this series with a pre-defined schedule.

Geometry and Mensuration: Test 18

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.

If loading fails, click here to try again

Congratulations - you have completed Geometry and Mensuration: Test 18.You scored %%SCORE%% out of %%TOTAL%%.You correct answer percentage: %%PERCENTAGE%% .Your performance has been rated as %%RATING%%

Your answers are highlighted below.

Question 1

An angle is equal to 1/3^rd of its supplement. Find its measure.

A	60^o
B	80^o
C	90^o
D	45^o

Question 1 Explanation:

$\displaystyle \begin{array}{l}\begin{array}{*{35}{l}} Let\text{ }that\text{ }angle\text{ }be\text{ }p \\ Supplement\text{ }of\text{ }this\text{ }angle\text{ }=\text{ }180-p \\ \end{array}\\Therefore\,\,\,p=\frac{1}{3}\,\left( 180-p \right)\\\Rightarrow 3p=180-p\\\Rightarrow p={{45}^{o}}\end{array}$

Question 2

In a triangle ABC, ∠A = 90^o and D is mid-point of AC. The value of BC² – BD² is equal to

A	AD²
B	2AD²
C	3AD²
D	4AD²

Question 2 Explanation:

BC² = AB² + AC²
BD² = AB² + AD²
BC² – BD² = AB² + AC² – AB² –AD²
= AC² – AD²
= (AC– AD) (AC + AD)
=(2AD – AD) (2AD + AD)
= AD × 3AD = 3AD²

Question 3

The in-radius of an equilateral triangle is of length 3 cm. Then the length of each of its medians is

A	12 cm
B	9/2 cm
C	4 cm
D	9 cm

Question 3 Explanation:

In equilateral triangle centroid, incentre,
orthocenter coincide at the same points
Height/3 = inradius
Therefore Height= Median= 3×3= 9 cm.

Question 4

If ABC is an equilateral triangle and D is a point on BC such that AD⊥BC ,then

A	AB: BD= 1: 1
B	AB: BD= 1: 2
C	AB: BD= 2: 1
D	AB: BD= 3: 2

Question 4 Explanation:

Let AB = 2 unit.
As the triangle is an equilateral triangle, the perpendicular from A will bisect BC. (in this case at D) BD = 1 unit.
Required ratio AB: BD= 2: 1.
Correct option is (c)

Question 5

A ladder leans against a vertical wall. The top of the ladder is 8m above the ground. When the bottom of the ladder is moved 2 m farther away from the wall, the top of the ladder rests against the foot of the wall. What is the length of the ladder?

A	10 m
B	15 m
C	20 m
D	17 m

Question 5 Explanation:

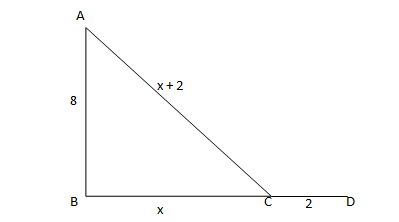
geometry-and-mensuration-test-18-question-5-pic-1-1

Let AB be the wall and AC is the ladder with C as the foot of the ladder.
Let BC = x and CD = 2. So the length of the ladder is x + 2 i.e. AC = x + 2.
Now in ΔABC, we have (x + 2)² = x² + 64
=> x² + 4 + 4x = x² + 64
=> 4x = 60 => x = 15m.
Hence the length of the ladder = 15 + 2 = 17m.

Once you are finished, click the button below. Any items you have not completed will be marked incorrect. Get Results

There are 5 questions to complete.

←

List

→

Return

Shaded items are complete.